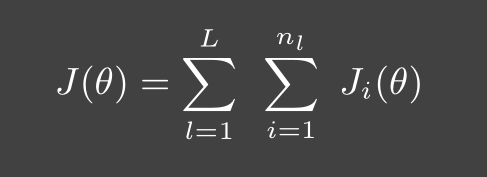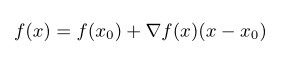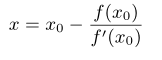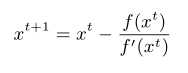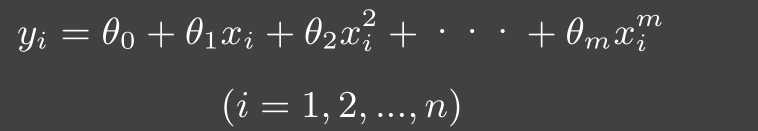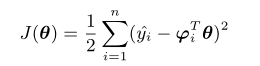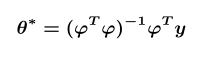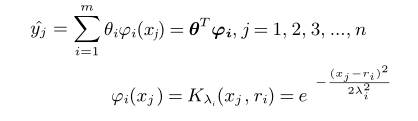回归模型

回归模型

1. 有监督学习

1.1 线性回归

1.1.1 正规方程法

  • $ h(X_i;\theta)=\theta_1x_1+\theta_2x_2+\theta_3x_3=x^T\theta$

  • 均方误差: $ MSE = \frac{1}{n}\sum_{i=1}^n(y_i-h(X_i))^2$

  • 最小化损失函数：$ argminL(\theta)=\frac{1}{n}\sum_{i=1}^n(y_i-h(X_i;\theta))^2$

  • 求解最优参数即求解最小化损失函数

    1. 构建损失函数
    2. 对损失函数求导（一阶偏导数即梯度 Gradient），令其等于0
    3. 求解二阶偏导数（黑塞矩阵 Hessian矩阵），判断极值情况，$ X^TX>=0$时，取极小值$ \theta$
    4. 求参数θ: $ \theta = (X^TX)^{-1}X^Ty$ (要求$ X^TX$可逆（列满秩）,若不可逆则需要正则化)
    1
    2
    import numpy as np
    w = np.linalg.inv(X.T@X)@X.T@y

1.1.2 梯度下降法（Gradient Descent）

  • 选定一个初始点，从初始点开始沿着梯度的负方向移动，直至收敛
  • image-20230702103526631
  • 设 $ f(x)=x^2-1$ , 则迭代函数为$ x_{k}=x_{k-1}-\alpha∇xf(x{k-1})$
  • $ ∇xf(x{k-1})=2x$
  • 假设$x_0=3,\alpha=0.6$
  • 按迭代函数迭代，最终找到一个无限趋近于0的值，在一定范围内则认为它是最优解
  • 注意：
    1. 学习率
    2. 初始点
    3. 目标函数
  • 以上三个都会影响最终的效率，可能导致梯度下降失效
  • 缺点
    • 每次迭代==整个数据集==，一旦样本量较大时，计算梯度的时间开销会变大

1.1.3 随机梯度下降法（Stochastic Gradient Descent）

  1. 在随机梯度下降中，我们每一次迭代更新 θ，都只考虑其中==一个样本==对应的损失函数 $ J_i(θ)$。通过这种方法，我们用 $ ∇θJ_i(θ) = (y_i− x^⊤_iθ)x_i$来近似 $ ∇_θJ(θ)$

    image-20230702104216474

  2. 停机准则：

    • ==最大迭代数T==：迭代数超过T，则算法停止
    • ==提前设定一个阈值==：系数与前一代相比的改进低于这个阈值（认为本次迭代产生了相反的效果），则算法停止
    • ==损失函数值==：当损失函数十分趋近于0时，算法停止

1.1.4 小批量梯度下降法（Mini-Batch GD）

  1. 我们将数据分为一共 B 个块 {$x^{(1)}, x^{(2)},··· ,x^{(L)}$}，其中每一块的样本数量为 $ n_1, n_2, · · · , n_L$。然后在更新系数时综合考虑一个块内的数据，算法遍历每个数据块。这时损失函数可以表示为

image-20230702104409181

  1. 小批量梯度下降算法的伪代码如下：image-20230702104552285
  2. 要求：
    1. 使每个块的样本数都相同
    2. 通过调整B块的大小，调整算法效率
    3. 块中样本数为1时，则为随机梯度下降算法
  3. 更适合在线学习: 因为数据是不断变化的，理论上来讲数据集是无限大的，此时用随机梯度下降算法，更新系数的成本十分大（每次更新数据都要更新系数）；此时用小批量梯度下降算法则更新系数时，仅需要部分样本
  4. 梯度下降算法的收敛性分析（==待完善==）
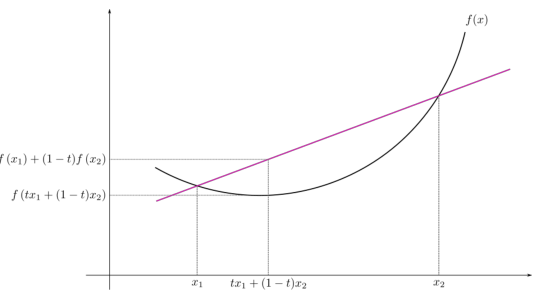
    • 凸函数

image-20231009002328274

image-20231009002347198

  • 利普希兹连续

    image-20231009002421876

1.1.5 牛顿法

  1. 牛顿法用迭代和不断逼近的思想来求解一个比较复杂的方程的根

  2. 牛顿法的核心思想是对函数的一阶泰勒展开求解

    image-20231009002622219

    将$ f(x)=0$代入

    image-20231009002701385

    在近似解x处一阶展开，更新近似解x的值，我们得到一个迭代方程

    image-20231009002950057

  3. 利用迭代方法逼近最优解以解 f(x) = 0

2.1 非线性回归

2.1.1 多项式回归

  1. 通常多项式回归模型函数的形式为image-20230702105032915
  2. 标准方程法
  3. 其损失函数为image-20231009084042377
  4. 用最小二乘法求得最优解为image-20231009084240799

2.1.2 径向基回归

1
径向基函数: 是一个取值仅依赖于到原点距离的实值函数，f(x)=f(|x|),任一满足f(x)=f(|x|)的函数都可称之为径向函数
  1. 高斯核函数
    • 表达式image-20231009085307352
    • $ \lambda_i为方差，r_i为均值$
    • 随着均值和方差的变化，高斯函数会随着发生变化，数据拟合的曲线是均值方差不同的高斯分布函数，由于e的指数函数的值必大于0，用标准方程法，得到其最优解为 $ \theta^* = (\varphi^T\varphi)^{-1}\varphi^Ty$

2.1.3 正则化

1
在前面的线性回归问题中，用正规方程法得到的参数值θ,当(X^TX)不可逆时，无法使用正规方程法，此时我们可以用正则化的方式处理
  1. 岭回归
  2. 套索回归
  3. 弹性网络
  4. 收缩估计器
  5. 参数选择

总结

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
无监督学习:从给定数据集中学习出一个函数（模型），对于新的数据，可以通过这个函数或模型预测结果

回归问题
	数据特征: 向量X
	标签: y
	通过训练集的数据组成的向量X,拟合一个函数y=wX+b
	使得预测值y与真实值的误差最小
		线性回归: 回归函数为一条直线或一个平面
			特点: 建模速度快、异常值敏感
		非线性回归: 回归函数是一条曲线或一个曲面
分类问题
	数据特征: 向量X
	标签: y
	通过训练集的数据组成的向量X,拟合一个函数y=wX+b
	使得真实值-预测值y为正数，则归为正类； 使得真实值-预测值y为负数，则归为负类
  1. 数据预处理
    • 标准化
    • 归一化
  2. 牛顿法和梯度下降法的比较
    • 梯度下降法考虑一阶函数，而牛顿法考虑二阶函数；梯度下降法仅考虑当前位置的坡度，而牛顿法不仅考虑当前位置，还考虑下一步的坡度
    • 梯度下降法要计算梯度，而牛顿法要计算二阶导数矩阵及其逆，因此牛顿法复杂度更高
    • 梯度下降算法要设置学习率，牛顿法不需要，省去了调参时间